| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 10 Circles
This section provides comprehensive solutions and explanations for Chapter 10: Circles. Circles represent one of the most fundamental and fascinating shapes in geometry, possessing unique properties and leading to a wide array of important theorems. This chapter delves into the intricate relationships between various components of a circle, including chords, arcs, the angles they form, and special types of quadrilaterals inscribed within them, known as cyclic quadrilaterals. The solutions aim to provide clarity, rigorous proofs, and practical applications of these core geometric concepts, enhancing your understanding beyond simple definitions.
Before diving into complex theorems, we revisit and solidify our understanding of essential terminology associated with circles: the center (the defining point equidistant from all points on the circle), radius (the distance from the center to any point on the circle), diameter (a chord passing through the center, equal to twice the radius), chord (a line segment connecting any two points on the circle), arc (a portion of the circumference, classified as major or minor), sector (a region bounded by two radii and the intercepted arc), segment (a region bounded by a chord and its intercepted arc), and the circumference (the total distance around the circle).
The core of this chapter, meticulously detailed in the solutions, revolves around several key theorems and their proofs:
- Equal chords within the same circle (or in congruent circles) are proven to subtend equal angles at the center. The converse is also true: if the angles subtended by chords at the center are equal, the chords themselves must be equal.
- A critical property: the perpendicular line segment drawn from the center of a circle to any chord invariably bisects the chord. The converse also holds: the line joining the center to the mid-point of a chord is perpendicular to that chord. Solutions frequently leverage this theorem, often in conjunction with the Pythagorean theorem ($a^2 + b^2 = c^2$), to calculate lengths related to chords, radii, and distances from the center.
- A fundamental construction principle: through any three given non-collinear points, there exists one and only one circle that passes through all of them.
- Relationship between chord length and distance from the center: Equal chords of a circle (or of congruent circles) are always equidistant from the center. The converse is also established: chords that are equidistant from the center must be equal in length.
- A highly significant theorem concerning angles: The angle subtended by an arc at the center of the circle is precisely double the angle subtended by the same arc at any point on the remaining part of the circle's circumference. This theorem is a cornerstone for solving many angle-related problems in circles.
- A direct consequence of the previous theorem: Angles subtended by the same arc in the same segment of a circle are always equal.
- A special case: The angle inscribed in a semicircle (an angle subtended by the diameter) is always a right angle ($90^{\circ}$).
- Properties of Cyclic Quadrilaterals (quadrilaterals whose four vertices lie on the circumference of a circle): The primary property is that the sum of either pair of opposite angles is always $180^{\circ}$. The converse is also vital: if the sum of a pair of opposite angles in a quadrilateral is $180^{\circ}$, then that quadrilateral must be cyclic.
Throughout the solutions for Chapter 10, students are guided through a multitude of problems. These exercises require the astute application of one or, more often, a combination of these theorems to determine unknown angles, calculate lengths, or construct logical proofs about geometric relationships involving circles. A strong emphasis is placed on clear reasoning and the precise justification of each step by referencing the appropriate theorem.
Exercise 10.1
Question 1. Fill in the blanks:
(i) The centre of a circle lies in ________of the circle. (exterior/ interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies_________` in of the circle. (exterior/ interior)
(iii) The longest chord of a circle is a_________ of the circle.
(iv) An arc is a_______ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and__________ of the circle.
(vi) A circle divides the plane, on which it lies, in___________ parts.
Answer:
(i) The centre of a circle lies in interior of the circle. (exterior/ interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies exterior in of the circle. (exterior/ interior)
(iii) The longest chord of a circle is a diameter of the circle.
(iv) An arc is a semicircle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and chord of the circle.
(vi) A circle divides the plane, on which it lies, in three parts.
Question 2. Write True or False: Give reasons for your answers.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Answer:
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
Answer: True
Reason: By the definition of a circle, a radius is a line segment that connects the center of the circle to any point on its circumference. The statement given is the exact definition of a radius.
(ii) A circle has only finite number of equal chords.
Answer: False
Reason: A circle is composed of an infinite number of points. For any given length less than or equal to the diameter, we can draw an infinite number of chords. For example, we can pick any point on the circle and draw a chord of a specific length. By rotating this chord around the center of the circle, we can find infinitely many chords of the same length.
(iii) If a circle is divided into three equal arcs, each is a major arc.
Answer: False
Reason: A full circle corresponds to an angle of $360^\circ$. If it is divided into three equal arcs, each arc will subtend an angle of $\frac{360^\circ}{3} = 120^\circ$ at the center. A major arc is an arc that subtends an angle greater than $180^\circ$ at the center. Since $120^\circ < 180^\circ$, each of these arcs is a minor arc, not a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Answer: True
Reason: The diameter of a circle is defined as the longest chord that passes through the center. Its length is equal to twice the radius ($d = 2r$). The statement describes a chord of length $2r$, which is precisely the definition of a diameter.
(v) Sector is the region between the chord and its corresponding arc.
Answer: False
Reason: The region between a chord and its corresponding arc is called a segment of the circle. A sector is the region of the circle enclosed by two radii and their intercepted arc.
(vi) A circle is a plane figure.
Answer: True
Reason: A circle is a two-dimensional figure defined as the set of all points in a plane that are equidistant from a fixed point (the center). Since it can be drawn entirely on a flat plane, it is a plane figure.
Exercise 10.2
Question 1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer:
Here is a diagram representing the given information:
Given:
Two congruent circles, let's call them $C_1$ and $C_2$, with centres $O$ and $O'$ respectively.
Since the circles are congruent, their radii are equal. Let the radius be $r$.
OA = OB = $r$
(Radii of circle $C_1$)
O'C = O'D = $r$
(Radii of circle $C_2$)
$AB$ is a chord of circle $C_1$ and $CD$ is a chord of circle $C_2$.
$AB = CD$
(Given that the chords are equal)
To Prove:
The angles subtended by these chords at their respective centres are equal.
That is, $\angle AOB = \angle CO'D$.
Proof:
Consider $\triangle AOB$ in circle $C_1$ and $\triangle CO'D$ in circle $C_2$.
OA = O'C
(Radii of congruent circles, both equal to $r$)
OB = O'D
(Radii of congruent circles, both equal to $r$)
AB = CD
(Given)
Thus, by the Side-Side-Side (SSS) congruence criterion, the two triangles are congruent.
$\triangle AOB \cong \triangle CO'D$
Since the triangles are congruent, their corresponding parts must be equal (CPCT - Corresponding Parts of Congruent Triangles).
Therefore,
$\angle AOB = \angle CO'D$
(By CPCT)
This proves that equal chords of congruent circles subtend equal angles at their centres.
Hence Proved.
Question 2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer:
Here is a diagram representing the given information:
Given:
Two congruent circles, let's call them $C_1$ and $C_2$, with centres $O$ and $O'$ respectively.
Since the circles are congruent, their radii are equal. Let the radius be $r$.
OA = OB = $r$
(Radii of circle $C_1$)
O'C = O'D = $r$
(Radii of circle $C_2$)
$AB$ is a chord of circle $C_1$ and $CD$ is a chord of circle $C_2$.
The angles subtended by the chords at their respective centres are equal.
$\angle AOB = \angle CO'D$
(Given)
To Prove:
The lengths of the chords are equal.
That is, $AB = CD$.
Proof:
Consider $\triangle AOB$ in circle $C_1$ and $\triangle CO'D$ in circle $C_2$.
OA = O'C
(Radii of congruent circles, both equal to $r$)
OB = O'D
(Radii of congruent circles, both equal to $r$)
$\angle AOB = \angle CO'D$
(Given)
Thus, by the Side-Angle-Side (SAS) congruence criterion, the two triangles are congruent.
$\triangle AOB \cong \triangle CO'D$
Since the triangles are congruent, their corresponding parts must be equal (CPCT - Corresponding Parts of Congruent Triangles).
Therefore,
AB = CD
(By CPCT)
This proves that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Hence Proved.
Example 1 (Before Exercise 10.3)
Example 1. Given an arc of a circle, complete the circle.
Answer:
Given:
An arc $PQ$ of a circle.
Construction Required:
To complete the circle from the given arc $PQ$.
Steps of Construction:
1. Take any three distinct points $A$, $B$, and $C$ on the given arc $PQ$.
2. Join points $A$ and $B$ to form the chord $AB$.
3. Join points $B$ and $C$ to form the chord $BC$.
4. Construct the perpendicular bisector of the chord $AB$. Let this be $LM$.
5. Construct the perpendicular bisector of the chord $BC$. Let this be $RS$.
6. Let the two perpendicular bisectors $LM$ and $RS$ intersect at a point $O$.
7. Take the point $O$ as the centre of the circle.
8. Measure the distance from $O$ to any of the points $A$, $B$, or $C$. This distance $OA$ (or $OB$ or $OC$) is the radius $r$ of the circle.
9. With centre $O$ and radius $r = OA$, draw the circle. This circle will pass through points $A$, $B$, and $C$ and is the required completion of the arc $PQ$.
Justification:
We know that the perpendicular bisector of any chord of a circle passes through the centre of the circle.
Since $A$, $B$, and $C$ are points on the arc (and thus on the circle to be completed), $AB$ and $BC$ are chords of the required circle.
The perpendicular bisector $LM$ of chord $AB$ must pass through the centre.
Similarly, the perpendicular bisector $RS$ of chord $BC$ must also pass through the centre.
Since the points $A$, $B$, and $C$ are not collinear (they lie on an arc), the chords $AB$ and $BC$ are not parallel.
Therefore, their perpendicular bisectors $LM$ and $RS$ are also not parallel and will intersect at a unique point.
This unique point of intersection, $O$, must be the centre of the circle.
The distance from the centre $O$ to any point on the arc ($A$, $B$, or $C$) is the radius $r$.
Hence, the circle drawn with centre $O$ and radius $r=OA$ is the required completed circle.
Exercise 10.3
Question 1. Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer:
We can draw different pairs of circles, and the number of common points they have depends on their relative positions.
Case 1: The circles do not intersect (0 common points)
This can happen when the circles are completely separate or when one is entirely inside the other.
Number of common points = 0.
Case 2: The circles touch at exactly one point (1 common point)
This can happen when the circles touch each other externally or internally.
Number of common points = 1.
Case 3: The circles intersect at two distinct points (2 common points)
In this case, the circles overlap, crossing each other at two locations.
Number of common points = 2.
If we consider two different circles, these are the only possibilities for the number of intersection points.
The possible numbers of common points are 0, 1, or 2.
The maximum number of common points for a pair of circles is the largest number from the possibilities.
Therefore, the maximum number of common points is 2.
Question 2. Suppose you are given a circle. Give a construction to find its centre.
Answer:
To find the centre of a given circle, we can use the property that the perpendicular bisector of a chord of a circle passes through the centre.
Construction:
Step 1: Take any three distinct points P, Q, and R on the circumference of the given circle.
Step 2: Join points P and Q to form a chord PQ.
Step 3: Join points Q and R to form another chord QR.
Step 4: Construct the perpendicular bisector of the chord PQ.
To do this: With P as the centre and a radius greater than half of PQ, draw arcs on both sides of PQ. With Q as the centre and the same radius, draw arcs intersecting the previous arcs at points A and B. Join A and B. The line segment AB is the perpendicular bisector of PQ.
Step 5: Construct the perpendicular bisector of the chord QR.
To do this: With Q as the centre and a radius greater than half of QR, draw arcs on both sides of QR. With R as the centre and the same radius, draw arcs intersecting the previous arcs at points C and D. Join C and D. The line segment CD is the perpendicular bisector of QR.
Step 6: The point where the perpendicular bisectors AB and CD intersect is the centre of the circle.
Let the point of intersection of AB and CD be O.
Verification:
Since AB is the perpendicular bisector of chord PQ, any point on AB is equidistant from P and Q. Thus, OP = OQ.
Since CD is the perpendicular bisector of chord QR, any point on CD is equidistant from Q and R. Thus, OQ = OR.
From these two equalities, we have OP = OQ = OR. This means that the point O is equidistant from the three points P, Q, and R on the circumference of the circle. Therefore, O is the centre of the circle.
Question 3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer:
Given:
Two circles with centres O and O' intersect at two distinct points A and B.
To Prove:
The centres O and O' lie on the perpendicular bisector of the common chord AB.
Proof:
Consider the circle with centre O.
A and B are points on the circumference of this circle.
OA = OB
(Radii of the same circle)
Since O is equidistant from A and B, O must lie on the perpendicular bisector of the line segment AB.
Now, consider the circle with centre O'.
A and B are points on the circumference of this circle.
O'A = O'B
(Radii of the same circle)
Since O' is equidistant from A and B, O' must lie on the perpendicular bisector of the line segment AB.
Since both centres O and O' lie on the perpendicular bisector of the line segment AB, the line segment joining the centres (OO') is the perpendicular bisector of the common chord AB.
Therefore, the centres of the two circles lie on the perpendicular bisector of the common chord.
Example 2 (Before Exercise 10.4)
Example 2. If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.
Answer:
Given:
Let's consider a circle with centre O.
AB and CD are two chords of the circle which intersect at a point E.
PQ is a diameter of the circle which passes through the point of intersection E.
The chords AB and CD make equal angles with the diameter PQ, which means $\angle AEQ = \angle DEQ$.
To Prove:
The chords are equal, i.e., $AB = CD$.
Construction:
From the centre O, draw perpendiculars to the chords AB and CD.
Let $OL \perp AB$ and $OM \perp CD$.
Proof:
In the triangles $\triangle OLE$ and $\triangle OME$, we have:
$\angle OLE = \angle OME$
(Each $90^\circ$, by construction)
OE = OE
(Common side)
$\angle LEO = \angle MEO$
(Given as $\angle AEQ = \angle DEQ$)
Therefore, by the AAS (Angle-Angle-Side) congruence rule, we have:
$\triangle OLE \cong \triangle OME$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we get:
OL = OM
This means that the chords AB and CD are equidistant from the centre O.
We know a fundamental property of circles: Chords that are equidistant from the centre of a circle are equal in length.
Hence, $AB = CD$.
Thus, it is proved that if two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, then the chords are equal.
Exercise 10.4
Question 1. Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Answer:
Given:
Two circles intersect at two points.
Radius of the first circle, $r_1 = 5$ cm.
Radius of the second circle, $r_2 = 3$ cm.
The distance between their centres, $d = 4$ cm.
To Find:
The length of the common chord.
Solution:
Let the two circles have centres O and O' respectively. Let the radii be $OA = 5$ cm and $O'A = 3$ cm. The distance between the centres is $OO' = 4$ cm. Let the common chord be AB.
Consider the triangle $\triangle OAO'$. The lengths of its sides are $OA = 5$ cm, $O'A = 3$ cm, and $OO' = 4$ cm.
We will use the converse of the Pythagorean theorem to check if $\triangle OAO'$ is a right-angled triangle.
$O'A^2 + OO'^2 = (3)^2 + (4)^2$
$ = 9 + 16 = 25$
$OA^2 = (5)^2 = 25$
Since $O'A^2 + OO'^2 = OA^2$, the triangle $\triangle OAO'$ is a right-angled triangle, with the right angle at vertex O'.
$\therefore \angle AO'O = 90^\circ$
We know that the line segment joining the centres of two intersecting circles is the perpendicular bisector of their common chord. Let M be the point of intersection of the common chord AB and the line segment OO'.
Thus, $AM \perp OO'$ and $AB = 2 \times AM$.
Now, let's find the area of $\triangle OAO'$. Since it is a right-angled triangle, its area can be calculated as:
Area($\triangle OAO'$) = $\frac{1}{2} \times \text{Base} \times \text{Height}$
$= \frac{1}{2} \times O'O \times O'A = \frac{1}{2} \times 4 \times 3 = 6 \text{ cm}^2$
...(i)
Also, the area of $\triangle OAO'$ can be calculated by taking OO' as the base and AM as the corresponding altitude.
Area($\triangle OAO'$) = $\frac{1}{2} \times OO' \times AM$
...(ii)
From equations (i) and (ii), we get:
$\frac{1}{2} \times 4 \times AM = 6$
$2 \times AM = 6$
$AM = \frac{6}{2} = 3$ cm
The length of the common chord AB is twice the length of AM.
$AB = 2 \times AM = 2 \times 3 = 6$ cm
Alternate Solution:
We can find the area of $\triangle OAO'$ using Heron's formula.
The sides of the triangle are $a = 5$ cm, $b = 3$ cm, and $c = 4$ cm.
First, we find the semi-perimeter (s) of the triangle:
$s = \frac{a+b+c}{2} = \frac{5+3+4}{2} = \frac{12}{2} = 6$ cm
Now, we apply Heron's formula to find the area:
Area = $\sqrt{s(s-a)(s-b)(s-c)}$
Area = $\sqrt{6(6-5)(6-3)(6-4)}$
Area = $\sqrt{6 \times 1 \times 3 \times 2} = \sqrt{36} = 6 \text{ cm}^2$
Let AM be the altitude from vertex A to the base OO'. The length of AM is half the length of the common chord.
Area of $\triangle OAO'$ can also be expressed as:
Area = $\frac{1}{2} \times \text{Base} \times \text{Altitude} = \frac{1}{2} \times OO' \times AM$
$6 = \frac{1}{2} \times 4 \times AM$
$6 = 2 \times AM$
$AM = 3$ cm
The length of the common chord is $AB = 2 \times AM$.
$AB = 2 \times 3 = 6$ cm
Final Answer: The length of the common chord is 6 cm.
Question 2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Answer:
Given:
A circle with centre O.
Two equal chords AB and CD intersect within the circle at a point E.
AB = CD
(Given)
To Prove:
The corresponding segments of the chords are equal.
That is, AE = DE and CE = BE.
Construction:
From the centre O, draw perpendiculars to the chords AB and CD.
Draw $OM \perp AB$ and $ON \perp CD$.
Join OE.
Proof:
We know that equal chords of a circle are equidistant from the centre.
Since AB = CD, we have:
OM = ON
[Chords equidistant from centre] ... (i)
Now, in the right-angled triangles $\triangle OME$ and $\triangle ONE$, we have:
$\angle OME = \angle ONE$
(Each $90^\circ$, by construction)
OE = OE
(Common hypotenuse)
OM = ON
(From equation (i))
Therefore, by the RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle OME \cong \triangle ONE$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we get:
ME = NE
... (ii)
We also know that the perpendicular drawn from the centre of a circle to a chord bisects the chord.
So, $AM = MB = \frac{1}{2}AB$ and $CN = ND = \frac{1}{2}CD$.
Since it is given that $AB = CD$, it follows that their halves are also equal:
$\frac{1}{2}AB = \frac{1}{2}CD$
$\implies AM = ND$
... (iii)
and $MB = CN$
... (iv)
Now, to prove the first part, we add equations (iii) and (ii):
$AM + ME = ND + NE$
From the figure, we can see that $AM + ME = AE$ and $ND + NE = DE$.
$\implies AE = DE$
Next, to prove the second part, we subtract equation (ii) from equation (iv):
$MB - ME = CN - NE$
From the figure, we can see that $MB - ME = BE$ and $CN - NE = CE$.
$\implies BE = CE$
Thus, the segments of one chord are equal to the corresponding segments of the other chord.
Hence Proved.
Question 3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer:
Given:
A circle with centre O.
Two equal chords AB and CD intersect within the circle at a point E.
AB = CD
(Given)
To Prove:
The line joining the point of intersection to the centre (OE) makes equal angles with the chords.
That is, $\angle OEA = \angle OED$.
Construction:
From the centre O, draw perpendiculars to the chords AB and CD.
Draw $OM \perp AB$ and $ON \perp CD$.
Proof:
We are given that AB and CD are equal chords. We know that equal chords of a circle are equidistant from the centre.
OM = ON
[Equal chords are equidistant from the centre] ... (i)
Now, consider the right-angled triangles $\triangle OME$ and $\triangle ONE$:
$\angle OME = \angle ONE$
(Each $90^\circ$, by construction)
OE = OE
(Common hypotenuse)
OM = ON
(From equation (i))
Therefore, by the RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle OME \cong \triangle ONE$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we get:
$\angle OEM = \angle OEN$
Since M is on the chord AB and N is on the chord CD, these are the angles that the line OE makes with the chords AB and CD.
Thus, the line joining the point of intersection to the centre makes equal angles with the chords.
Hence Proved.
Question 4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Fig. 10.25).
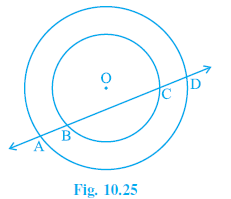
Answer:
Given:
Two concentric circles with a common centre O.
A line intersects the outer circle at points A and D, and the inner circle at points B and C.
To Prove:
AB = CD.
Construction:
From the centre O, draw a perpendicular to the line AD, intersecting it at point M.
So, $OM \perp AD$.
Proof:
We know that a perpendicular drawn from the centre of a circle to a chord bisects the chord.
For the inner circle, BC is the chord and $OM \perp BC$.
Therefore, M is the midpoint of BC.
BM = CM
... (i)
For the outer circle, AD is the chord and $OM \perp AD$.
Therefore, M is the midpoint of AD.
AM = DM
... (ii)
Now, we subtract equation (i) from equation (ii):
AM - BM = DM - CM
From the figure, we can see that:
$AM - BM = AB$
$DM - CM = CD$
Therefore,
AB = CD
Hence Proved.
Question 5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Answer:
Given:
Three girls, Reshma (R), Salma (S), and Mandip (M), are standing on a circle with centre O and radius 5 m.
The distance between Reshma and Salma is 6 m, so the length of chord RS = 6 m.
The distance between Salma and Mandip is 6 m, so the length of chord SM = 6 m.
The radius of the circle is 5 m, so OR = OS = OM = 5 m.
To Find:
The distance between Reshma and Mandip, which is the length of the chord RM.
Solution:
Let's draw a diagram representing the positions of the girls and the centre of the circle.
Consider the triangles $\triangle ORS$ and $\triangle OMS$.
OR = OM
(Radii of the same circle, both 5 m)
RS = SM
(Given, both 6 m)
OS = OS
(Common side)
By the SSS (Side-Side-Side) congruence rule, we have:
$\triangle ORS \cong \triangle OMS$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we get:
$\angle ROS = \angle MOS$
Now, let's find the area of $\triangle ORS$. It's an isosceles triangle with sides 5 m, 5 m, and 6 m. Draw a perpendicular OA from the centre O to the chord RS. This perpendicular will bisect the chord RS.
$AR = AS = \frac{1}{2} \times RS = \frac{1}{2} \times 6 = 3$ m.
In the right-angled triangle $\triangle OAR$, using the Pythagorean theorem:
$OA^2 + AR^2 = OR^2$
$OA^2 + 3^2 = 5^2$
$OA^2 + 9 = 25$
$OA^2 = 25 - 9 = 16$
$OA = \sqrt{16} = 4$ m.
Now, we can calculate the area of $\triangle ORS$:
Area($\triangle ORS$) = $\frac{1}{2} \times \text{Base} \times \text{Height}$
$= \frac{1}{2} \times RS \times OA = \frac{1}{2} \times 6 \times 4 = 12 \text{ m}^2$
... (i)
Let the line segment OS intersect the chord RM at point K.
In $\triangle ORM$, since OR = OM (radii), it is an isosceles triangle. Since $\angle ROS = \angle MOS$, the line OK is the angle bisector of the vertex angle $\angle ROM$. In an isosceles triangle, the angle bisector of the vertex angle is also the perpendicular bisector of the base.
Therefore, $OK \perp RM$ and K is the midpoint of RM.
The length of the chord RM will be $2 \times RK$.
Now, consider the area of $\triangle ORS$ again, this time taking OS as the base and RK as the corresponding height (since RK is perpendicular to OS from R).
Area($\triangle ORS$) = $\frac{1}{2} \times \text{Base} \times \text{Height}$
$= \frac{1}{2} \times OS \times RK$
... (ii)
From equations (i) and (ii), we can equate the areas:
$\frac{1}{2} \times OS \times RK = 12$
We know that OS is the radius, so OS = 5 m.
$\frac{1}{2} \times 5 \times RK = 12$
$5 \times RK = 24$
$RK = \frac{24}{5} = 4.8$ m.
The distance between Reshma and Mandip is the length of the chord RM.
$RM = 2 \times RK = 2 \times 4.8 = 9.6$ m.
Final Answer: The distance between Reshma and Mandip is 9.6 m.
Question 6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Answer:
Given:
A circular park with centre O and radius 20 m.
Three boys Ankur (A), Syed (S), and David (D) are sitting at equal distances on its boundary.
This means the triangle formed by their positions, $\triangle ASD$, is an equilateral triangle.
The radius of the circle is $R = OA = OS = OD = 20$ m.
To Find:
The length of the string of each phone, which is the side length of the equilateral triangle $\triangle ASD$.
Solution:
Let the side length of the equilateral triangle be $a$. So, $AS = SD = DA = a$.
The circle is the circumcircle of the equilateral triangle $\triangle ASD$.
In an equilateral triangle, the circumcentre (centre of the circumscribing circle) and the centroid are the same point. Here, the centre of the circle, O, is the centroid of $\triangle ASD$.
Let's draw a median from vertex A to the midpoint M of the opposite side SD. The line segment AM is the median.
We know that the centroid of a triangle divides each median in the ratio 2:1, with the longer segment being from the vertex to the centroid.
So, for the median AM, the centroid O divides it such that:
AO : OM = 2 : 1
The length of AO is the radius of the circle, which is given as 20 m.
$\frac{AO}{OM} = \frac{2}{1}$
$\frac{20}{OM} = 2$
$OM = \frac{20}{2} = 10$ m
In an equilateral triangle, the median is also the altitude (perpendicular) to the opposite side. Therefore, $AM \perp SD$, which means $\angle OMS = 90^\circ$.
Now, consider the right-angled triangle $\triangle OMS$.
The hypotenuse is OS, which is the radius of the circle. So, $OS = 20$ m.
We have calculated $OM = 10$ m.
The side MS is half the length of the chord SD, so $MS = \frac{SD}{2} = \frac{a}{2}$.
Using the Pythagorean theorem in $\triangle OMS$:
$OM^2 + MS^2 = OS^2$
$10^2 + \left(\frac{a}{2}\right)^2 = 20^2$
$100 + \frac{a^2}{4} = 400$
$\frac{a^2}{4} = 400 - 100$
$\frac{a^2}{4} = 300$
$a^2 = 300 \times 4 = 1200$
$a = \sqrt{1200} = \sqrt{400 \times 3} = 20\sqrt{3}$ m
Final Answer: The length of the string of each phone is $20\sqrt{3}$ m.
Example 3 to 6 (Before Exercise 10.5)
Example 3. In Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠ AEB = 60°.
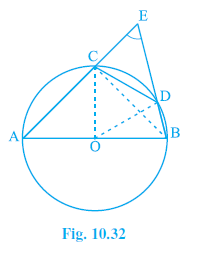
Answer:
Given:
A circle with centre O and diameter AB.
CD is a chord of the circle such that CD is equal to the radius of the circle.
AC and BD are extended to intersect at a point E outside the circle.
To Prove:
$\angle AEB = 60^\circ$.
Construction Required:
Join OC and OD.
Proof:
We are given that the chord CD is equal to the radius of the circle.
Let r be the radius of the circle. So, OC = OD = r.
CD = r
(Given)
In $\triangle OCD$, we have OC = OD = CD = r.
Therefore, $\triangle OCD$ is an equilateral triangle.
The angles of an equilateral triangle are all $60^\circ$.
$\angle COD = 60^\circ$
The angle subtended by an arc at the centre is double the angle subtended by the same arc at any point on the remaining part of the circle.
The measure of arc CD is equal to the angle it subtends at the centre.
Measure of arc CD = $\angle COD = 60^\circ$
AB is the diameter of the circle.
A diameter subtends an angle of $180^\circ$ at the centre, forming a semicircle.
The measure of the arc AB (the larger arc) is $180^\circ$.
Measure of arc AB = $180^\circ$
The angle formed by two secants intersecting outside a circle is half the difference of the measures of the intercepted arcs.
In this case, the lines AE (containing chord AC) and BE (containing chord BD) are secants from point E. They intercept arcs AB and CD.
$\angle AEB = \frac{1}{2}$ (Measure of arc AB - Measure of arc CD)
Substitute the measures of the arcs:
$\angle AEB = \frac{1}{2} (180^\circ - 60^\circ)$
$\angle AEB = \frac{1}{2} (120^\circ)$
$\angle AEB = 60^\circ$
Therefore, $\angle AEB = 60^\circ$.
Example 4. In Fig 10.33, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.
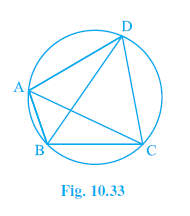
Answer:
Given:
ABCD is a cyclic quadrilateral.
AC and BD are its diagonals.
$\angle DBC = 55^\circ$
$\angle BAC = 45^\circ$
To Find:
The measure of $\angle BCD$.
Solution:
We know that angles in the same segment of a circle are equal.
Consider the chord CD. The angle subtended by chord CD at point B is $\angle DBC$. The angle subtended by chord CD at point A is $\angle CAD$. These angles are in the same segment.
$\angle CAD = \angle DBC$
(Angles in the same segment)
$\angle CAD = 55^\circ$
Consider the chord BC. The angle subtended by chord BC at point A is $\angle BAC$. The angle subtended by chord BC at point D is $\angle BDC$. These angles are in the same segment.
$\angle BDC = \angle BAC$
(Angles in the same segment)
$\angle BDC = 45^\circ$
Now, consider the triangle $\triangle BCD$. The sum of angles in a triangle is $180^\circ$.
$\angle BCD + \angle CDB + \angle DBC = 180^\circ$
(Angle sum property of a triangle)
Substitute the known values of $\angle CDB$ and $\angle DBC$:
$\angle BCD + 45^\circ + 55^\circ = 180^\circ$
$\angle BCD + 100^\circ = 180^\circ$
$\angle BCD = 180^\circ - 100^\circ$
$\angle BCD = 80^\circ$
Alternatively, using properties of cyclic quadrilaterals:
We found $\angle CAD = 55^\circ$ and $\angle BAC = 45^\circ$.
$\angle BAD = \angle BAC + \angle CAD = 45^\circ + 55^\circ = 100^\circ$.
In a cyclic quadrilateral, the sum of opposite angles is $180^\circ$.
$\angle BAD + \angle BCD = 180^\circ$
(Opposite angles of a cyclic quadrilateral)
$100^\circ + \angle BCD = 180^\circ$
$\angle BCD = 180^\circ - 100^\circ$
$\angle BCD = 80^\circ$
The measure of $\angle BCD$ is $80^\circ$.
Example 5. Two circles intersect at two points A and B. AD and AC are diameters to the two circles (see Fig.10.34). Prove that B lies on the line segment DC.

Answer:
Given:
Two circles intersect at points A and B.
AD is a diameter of one circle.
AC is a diameter of the other circle.
To Prove:
B lies on the line segment DC.
Proof:
Consider the circle with diameter AD. Since angle in a semicircle is a right angle, the angle subtended by the diameter AD at any point on the circumference is $90^\circ$. Point B lies on this circle.
$\angle$ABD = $90^\circ$
(Angle in a semicircle)
Now, consider the circle with diameter AC. Similarly, the angle subtended by the diameter AC at any point on the circumference is $90^\circ$. Point B also lies on this circle.
$\angle$ABC = $90^\circ$
(Angle in a semicircle)
Consider the angles $\angle$ABD and $\angle$ABC at point B.
These are adjacent angles sharing the common arm AB.
The sum of these angles is:
$\angle$ABD + $\angle$ABC = $90^\circ$ + $90^\circ$ = $180^\circ$.
Since the sum of the adjacent angles $\angle$ABD and $\angle$ABC is $180^\circ$, their non-common arms, BD and BC, form a straight line.
This means that points D, B, and C are collinear.
Therefore, B lies on the line segment DC.
Hence Proved.
Example 6. Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic.
Answer:
Given:
A quadrilateral ABCD.
The internal angle bisectors of $\angle A$, $\angle B$, $\angle C$, and $\angle D$ form another quadrilateral EFGH.
Specifically, let the bisectors of $\angle A$ and $\angle B$ intersect at E, $\angle B$ and $\angle C$ at F, $\angle C$ and $\angle D$ at G, and $\angle D$ and $\angle A$ at H.
To Prove:
The quadrilateral EFGH is a cyclic quadrilateral.
Proof:
To prove that EFGH is a cyclic quadrilateral, we need to show that the sum of a pair of its opposite angles is $180^\circ$. Let's aim to prove that $\angle EHG + \angle EFG = 180^\circ$.
Consider the triangle $\triangle AHD$. The sum of its angles is $180^\circ$.
$\angle AHD + \angle HAD + \angle HDA = 180^\circ$
[Angle sum property of a triangle]
Since AH and DH are the bisectors of $\angle A$ and $\angle D$ respectively:
$\angle HAD = \frac{1}{2}\angle A$ and $\angle HDA = \frac{1}{2}\angle D$.
Substituting these values in the equation above:
$\angle AHD + \frac{1}{2}\angle A + \frac{1}{2}\angle D = 180^\circ$
$\angle AHD = 180^\circ - \frac{1}{2}(\angle A + \angle D)$
The angle $\angle EHG$ of the quadrilateral EFGH is vertically opposite to $\angle AHD$.
$\angle EHG = \angle AHD$
(Vertically opposite angles)
$\therefore \angle EHG = 180^\circ - \frac{1}{2}(\angle A + \angle D)$
... (i)
Now, consider the triangle $\triangle BFC$. The sum of its angles is $180^\circ$.
$\angle BFC + \angle FBC + \angle FCB = 180^\circ$
[Angle sum property of a triangle]
Since BF and CF are the bisectors of $\angle B$ and $\angle C$ respectively:
$\angle FBC = \frac{1}{2}\angle B$ and $\angle FCB = \frac{1}{2}\angle C$.
Substituting these values:
$\angle BFC + \frac{1}{2}\angle B + \frac{1}{2}\angle C = 180^\circ$
$\angle BFC = 180^\circ - \frac{1}{2}(\angle B + \angle C)$
The angle $\angle EFG$ of the quadrilateral EFGH is the same as $\angle BFC$.
$\therefore \angle EFG = 180^\circ - \frac{1}{2}(\angle B + \angle C)$
... (ii)
Now, we add the two opposite angles of quadrilateral EFGH using equations (i) and (ii):
$\angle EHG + \angle EFG = \left[180^\circ - \frac{1}{2}(\angle A + \angle D)\right] + \left[180^\circ - \frac{1}{2}(\angle B + \angle C)\right]$
$\angle EHG + \angle EFG = 360^\circ - \frac{1}{2}(\angle A + \angle B + \angle C + \angle D)$
We know that the sum of the angles in the quadrilateral ABCD is $360^\circ$.
$\angle A + \angle B + \angle C + \angle D = 360^\circ$
(Angle sum property of a quadrilateral)
Substituting this value into our equation for the sum of angles:
$\angle EHG + \angle EFG = 360^\circ - \frac{1}{2}(360^\circ)$
$\angle EHG + \angle EFG = 360^\circ - 180^\circ$
$\angle EHG + \angle EFG = 180^\circ$
Since the sum of a pair of opposite angles of the quadrilateral EFGH is $180^\circ$, the quadrilateral EFGH is cyclic.
Hence Proved.
Exercise 10.5
Question 1. In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
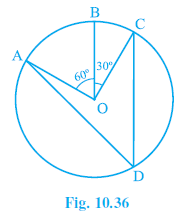
Answer:
Given:
A circle with centre O.
Points A, B, C are on the circle.
$\angle BOC = 30^\circ$
$\angle AOB = 60^\circ$
D is a point on the circle other than the arc ABC (meaning D is on the major arc AC).
To Find:
The measure of $\angle ADC$.
Solution:
The angle subtended by the arc AB at the centre is $\angle AOB = 60^\circ$.
The angle subtended by the arc BC at the centre is $\angle BOC = 30^\circ$.
The angle subtended by the arc AC at the centre is the sum of the angles subtended by arcs AB and BC at the centre, assuming B is between A and C on the minor arc.
$\angle AOC = \angle AOB + \angle BOC$
$\angle AOC = 60^\circ + 30^\circ$
$\angle AOC = 90^\circ$
The arc AC subtends the angle $\angle AOC$ at the centre and $\angle ADC$ at point D on the remaining part of the circle (which is the major arc ADC).
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
$\angle AOC = 2 \times \angle ADC$
Substitute the value of $\angle AOC$:
$90^\circ = 2 \times \angle ADC$
$\angle ADC = \frac{90^\circ}{2}$
$\angle ADC = 45^\circ$
The measure of $\angle ADC$ is $45^\circ$.
Question 2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Answer:
Given:
A circle with centre O.
Let AB be a chord of the circle such that its length is equal to the radius of the circle.
So, AB = OA = OB (where OA and OB are radii).
To Find:
1. The angle subtended by the chord AB at a point on the minor arc.
2. The angle subtended by the chord AB at a point on the major arc.
Solution:
Let's draw a diagram to represent the situation.
Consider the triangle $\triangle OAB$.
OA = OB
(Radii of the same circle)
AB = OA
(Given)
Therefore, $OA = OB = AB$.
Since all three sides of $\triangle OAB$ are equal, it is an equilateral triangle.
The angle subtended by the chord AB at the centre O is $\angle AOB$. In an equilateral triangle, all angles are equal to $60^\circ$.
$\therefore \angle AOB = 60^\circ$
1. Angle on the Major Arc
Let C be any point on the major arc. The angle subtended by the chord AB at point C is $\angle ACB$.
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
$\angle AOB = 2 \times \angle ACB$
$60^\circ = 2 \times \angle ACB$
$\angle ACB = \frac{60^\circ}{2} = 30^\circ$
So, the angle subtended by the chord at a point on the major arc is $30^\circ$.
2. Angle on the Minor Arc
Let D be any point on the minor arc. The angle subtended by the chord AB at point D is $\angle ADB$.
The points A, C, B, and D lie on the circle, forming a cyclic quadrilateral ACBD.
In a cyclic quadrilateral, the sum of opposite angles is $180^\circ$.
$\angle ACB + \angle ADB = 180^\circ$
Substituting the value of $\angle ACB$ we found earlier:
$30^\circ + \angle ADB = 180^\circ$
$\angle ADB = 180^\circ - 30^\circ = 150^\circ$
So, the angle subtended by the chord at a point on the minor arc is $150^\circ$.
Final Answer:
The angle subtended by the chord at a point on the minor arc is $150^\circ$.
The angle subtended by the chord at a point on the major arc is $30^\circ$.
Question 3. In Fig. 10.37, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
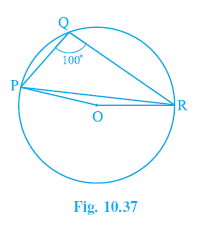
Answer:
Given:
P, Q, and R are points on a circle with centre O.
$\angle$PQR = $100^\circ$.
To Find:
$\angle$OPR.
Solution:
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
The angle $\angle$PQR is subtended by the minor arc PR at point Q on the remaining part of the circle.
The angle subtended by the minor arc PR at the centre is the reflex angle $\angle$POR.
Reflex $\angle$POR = 2 $\times \angle$PQR
Reflex $\angle$POR = 2 $\times 100^\circ = 200^\circ$.
The non-reflex angle $\angle$POR is $360^\circ$ - Reflex $\angle$POR.
$\angle$POR = $360^\circ - 200^\circ$
$\angle$POR = $160^\circ$.
Now, consider the triangle $\triangle$OPR.
OP = OR
(Radii of the same circle)
Therefore, $\triangle$OPR is an isosceles triangle.
In an isosceles triangle, the angles opposite the equal sides are equal.
$\angle$OPR = $\angle$ORP
In $\triangle$OPR, the sum of angles is $180^\circ$.
$\angle$POR + $\angle$OPR + $\angle$ORP = $180^\circ$
(Angle sum property of a triangle)
Substitute the values:
$160^\circ$ + $\angle$OPR + $\angle$OPR = $180^\circ$
$160^\circ$ + 2$\angle$OPR = $180^\circ$
2$\angle$OPR = $180^\circ - 160^\circ$
2$\angle$OPR = $20^\circ$
$\angle$OPR = $\frac{20^\circ}{2}$
$\angle$OPR = $10^\circ$
The value of $\angle$OPR is $10^\circ$.
Question 4. In Fig. 10.38, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
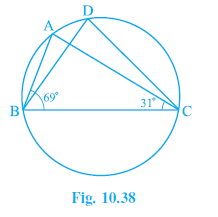
Answer:
Given:
Points A, B, C are on a circle.
$\angle ABC = 69^\circ$
$\angle ACB = 31^\circ$
D is a point on the circle.
To Find:
The measure of $\angle BDC$.
Solution:
Consider $\triangle ABC$. The sum of angles in a triangle is $180^\circ$.
$\angle BAC + \angle ABC + \angle ACB = 180^\circ$
Substitute the given values of $\angle ABC$ and $\angle ACB$:
$\angle BAC + 69^\circ + 31^\circ = 180^\circ$
$\angle BAC + 100^\circ = 180^\circ$
$\angle BAC = 180^\circ - 100^\circ$
$\angle BAC = 80^\circ$
We know that angles in the same segment of a circle are equal.
Consider the chord BC. The angle subtended by chord BC at point A is $\angle BAC$. The angle subtended by chord BC at point D is $\angle BDC$. These angles are in the same segment (the segment containing point A and point D).
$\angle BDC = \angle BAC$
Substitute the value of $\angle BAC$:
$\angle BDC = 80^\circ$
The measure of $\angle BDC$ is $80^\circ$.
Question 5. In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
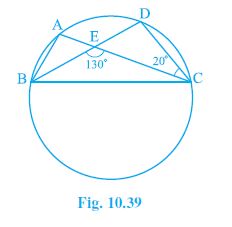
Answer:
Given:
A, B, C, and D are four points on a circle, forming a cyclic quadrilateral.
Diagonals AC and BD intersect at point E.
$\angle BEC = 130^\circ$
$\angle ECD = 20^\circ$
To Find:
The measure of $\angle BAC$.
Solution:
Consider the straight line BD. The angles $\angle BEC$ and $\angle CED$ are angles on a straight line, so they are supplementary.
$\angle BEC + \angle CED = 180^\circ$
(Linear pair)
Substitute the value of $\angle BEC$:
$130^\circ + \angle CED = 180^\circ$
$\angle CED = 180^\circ - 130^\circ$
$\angle CED = 50^\circ$
Now consider $\triangle CED$. The sum of angles in a triangle is $180^\circ$.
$\angle ECD + \angle CED + \angle CDE = 180^\circ$
(Angle sum property of a triangle)
Substitute the values of $\angle ECD$ and $\angle CED$:
$20^\circ + 50^\circ + \angle CDE = 180^\circ$
$70^\circ + \angle CDE = 180^\circ$
$\angle CDE = 180^\circ - 70^\circ$
$\angle CDE = 110^\circ$
So, $\angle CDB = 110^\circ$.
We know that angles in the same segment of a circle are equal.
Consider the chord BC. The angle subtended by chord BC at point A is $\angle BAC$. The angle subtended by chord BC at point D is $\angle BDC$. These angles are in the same segment.
$\angle BAC = \angle BDC$
Substitute the value of $\angle BDC$:
$\angle BAC = 110^\circ$
Question 6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Answer:
Given:
ABCD is a cyclic quadrilateral.
Diagonals AC and BD intersect at point E.
$\angle DBC = 70^\circ$
$\angle BAC = 30^\circ$
For the second part of the problem, it is given that AB = BC.
To Find:
1. The value of $\angle BCD$.
2. The value of $\angle ECD$ when AB = BC.
Solution:
Part 1: Finding $\angle BCD$
We know that angles subtended by the same arc at any point on the remaining part of the circle are equal. This is also known as the "angles in the same segment" property.
Consider the arc CD. It subtends $\angle DBC$ and $\angle DAC$ on the circumference.
$\angle DAC = \angle DBC$
(Angles in the same segment)
Since we are given $\angle DBC = 70^\circ$, we have:
$\angle DAC = 70^\circ$
Now, let's find the complete angle $\angle DAB$.
$\angle DAB = \angle DAC + \angle BAC$
Substituting the known values:
$\angle DAB = 70^\circ + 30^\circ = 100^\circ$
Since ABCD is a cyclic quadrilateral, we know that the sum of opposite angles is $180^\circ$.
$\angle DAB + \angle BCD = 180^\circ$
(Opposite angles of a cyclic quadrilateral)
Substituting the value of $\angle DAB$:
$100^\circ + \angle BCD = 180^\circ$
$\angle BCD = 180^\circ - 100^\circ$
$\angle BCD = 80^\circ$
Part 2: Finding $\angle ECD$ when AB = BC
Now, we are given the additional condition that AB = BC.
Consider the triangle $\triangle ABC$. Since two of its sides are equal (AB = BC), it is an isosceles triangle.
In an isosceles triangle, the angles opposite to the equal sides are also equal.
$\angle BCA = \angle BAC$
(Angles opposite to equal sides)
We are given that $\angle BAC = 30^\circ$.
$\therefore \angle BCA = 30^\circ$
We have already found that the entire angle $\angle BCD = 80^\circ$.
From the figure, we can see that:
$\angle BCD = \angle BCA + \angle ACD$
The angle $\angle ACD$ is the same as the angle $\angle ECD$.
$\angle BCD = \angle BCA + \angle ECD$
Substituting the values we have found:
$80^\circ = 30^\circ + \angle ECD$
$\angle ECD = 80^\circ - 30^\circ$
$\angle ECD = 50^\circ$
Final Answer:
The value of $\angle BCD$ is $80^\circ$.
Further, if AB = BC, the value of $\angle ECD$ is $50^\circ$.
Question 7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Answer:
Given:
ABCD is a cyclic quadrilateral.
The diagonals AC and BD are diameters of the circle passing through the vertices A, B, C, and D.
To Prove:
ABCD is a rectangle.
Proof:
To prove that a quadrilateral is a rectangle, we need to show that all its interior angles are $90^\circ$.
We know that the angle subtended by a diameter at any point on the circumference of the circle is a right angle ($90^\circ$). This is the "angle in a semicircle" theorem.
Consider AC as the diameter. The points B and D lie on the circumference.
$\angle ABC = 90^\circ$
(Angle in a semicircle)
$\angle ADC = 90^\circ$
(Angle in a semicircle)
Similarly, consider BD as the diameter. The points A and C lie on the circumference.
$\angle BAD = 90^\circ$
(Angle in a semicircle)
$\angle BCD = 90^\circ$
(Angle in a semicircle)
Since all four interior angles of the quadrilateral ABCD are $90^\circ$, it is a rectangle.
Hence Proved.
Alternate Method:
Let the centre of the circle be O. Since AC and BD are diameters, they must pass through the centre O and bisect each other at O.
AO = OC = BO = OD
(All are radii of the same circle)
Since the diagonals AC and BD are both diameters, their lengths are equal.
AC = BD
(Diameters of the same circle)
ABCD is a quadrilateral whose diagonals are equal and bisect each other. A quadrilateral with these properties is a rectangle.
Question 8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:
Given:
A trapezium ABCD in which AB $\parallel$ CD.
The non-parallel sides are equal, i.e., AD = BC.
To Prove:
Trapezium ABCD is cyclic.
Construction:
Draw perpendiculars from vertices A and B to the side CD. Let these be AM and BN respectively.
So, AM $\perp$ CD and BN $\perp$ CD.
Proof:
To prove that the trapezium is cyclic, we need to show that the sum of a pair of its opposite angles is $180^\circ$.
Consider the right-angled triangles $\triangle AMD$ and $\triangle BNC$.
AD = BC
(Given)
$\angle AMD = \angle BNC = 90^\circ$
(By construction)
AM and BN are the perpendicular distances between the two parallel lines AB and CD. The distance between two parallel lines is always constant.
AM = BN
(Distance between parallel lines)
Therefore, by the RHS (Right angle-Hypotenuse-Side) congruence rule:
$\triangle AMD \cong \triangle BNC$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), we get:
$\angle ADC = \angle BCD$
... (i)
That is, $\angle D = \angle C$.
Now, since AB $\parallel$ CD and AD is a transversal line intersecting them, the sum of the interior angles on the same side of the transversal is $180^\circ$.
$\angle DAB + \angle ADC = 180^\circ$
(Consecutive interior angles are supplementary)
That is, $\angle A + \angle D = 180^\circ$.
From equation (i), we can substitute $\angle D$ with $\angle C$ in the above equation:
$\angle A + \angle C = 180^\circ$
Since the sum of a pair of opposite angles of the trapezium ABCD is $180^\circ$, the trapezium is cyclic.
Hence Proved.
Question 9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP = ∠ QCD.

Answer:
Given:
Two circles intersect at two points B and C.
Two line segments ABD and PBQ are drawn through the point of intersection B, intersecting the circles at A, D and P, Q respectively.
To Prove:
$\angle ACP = \angle QCD$.
Proof:
We will use the property that angles in the same segment of a circle are equal.
For the first circle (containing points A, P, B, C):
The points A, C, P are on the circle. The arc AP subtends angles $\angle ACP$ and $\angle ABP$ on the circumference.
$\angle ACP = \angle ABP$
[Angles in the same segment] ... (i)
For the second circle (containing points Q, D, B, C):
The points Q, C, D are on the circle. The arc QD subtends angles $\angle QCD$ and $\angle QBD$ on the circumference.
$\angle QCD = \angle QBD$
[Angles in the same segment] ... (ii)
Now, consider the line segments ABD and PBQ which intersect at point B.
The angles $\angle ABP$ and $\angle QBD$ are vertically opposite angles.
We know that vertically opposite angles are equal.
$\angle ABP = \angle QBD$
[Vertically opposite angles] ... (iii)
From equations (i), (ii), and (iii), we can conclude that:
$\angle ACP = \angle ABP$
$\angle ABP = \angle QBD$
$\angle QBD = \angle QCD$
Therefore, by combining these equalities, we get:
$\angle ACP = \angle QCD$
Hence Proved.
Question 10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Answer:
Given:
A triangle ABC.
A circle is drawn with AB as diameter.
A circle is drawn with AC as diameter.
Let the two circles intersect at points A and D.
To Prove:
The point of intersection D (other than A) lies on the third side BC of the triangle ABC.
Construction:
Join AD.
Proof:
To prove that D lies on the line segment BC, we need to show that B, D, and C form a straight line. This can be done by proving that $\angle BDA + \angle CDA = 180^\circ$.
Consider the circle drawn with AB as diameter.
The angle subtended by a diameter at any point on the circumference is a right angle ($90^\circ$). This is the "angle in a semicircle" theorem.
Since D is a point on this circle, the angle subtended by the diameter AB at D is $\angle ADB$.
$\angle ADB = 90^\circ$
... (i)
Now consider the circle drawn with AC as diameter.
Since D is also a point on this second circle, the angle subtended by the diameter AC at D is $\angle ADC$.
$\angle ADC = 90^\circ$
... (ii)
Now, let's add the angles $\angle ADB$ and $\angle ADC$ from equations (i) and (ii):
$\angle ADB + \angle ADC = 90^\circ + 90^\circ$
$\angle BDC = 180^\circ$
Since the sum of the adjacent angles $\angle ADB$ and $\angle ADC$ is $180^\circ$, BDC is a straight line. Therefore, the points B, D, and C are collinear.
This proves that the point of intersection D lies on the third side BC.
Hence Proved.
Question 11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Answer:
Given:
ABC is a right triangle with $\angle ABC = 90^\circ$.
ADC is a right triangle with $\angle ADC = 90^\circ$.
AC is the common hypotenuse for both triangles.
To Prove:
$\angle CAD = \angle CBD$.
Proof:
We can think of AC as the diameter of a circle. The angle in a semicircle is always a right angle ($90^\circ$).
Since $\triangle ABC$ is a right triangle with $\angle B = 90^\circ$, the vertex B must lie on the circle whose diameter is the hypotenuse AC.
Similarly, since $\triangle ADC$ is a right triangle with $\angle D = 90^\circ$, the vertex D must also lie on the same circle whose diameter is the hypotenuse AC.
Since points A, B, C, and D all lie on the same circle, they are concyclic. This means that the quadrilateral ABCD is a cyclic quadrilateral.
Now, consider the chord CD of this circle.
The angles subtended by the same chord (or arc) at any point on the circumference in the same segment are equal.
The chord CD subtends $\angle CAD$ and $\angle CBD$ at points A and B on the circumference.
Since A and B are in the same segment with respect to the chord CD, the angles must be equal.
$\angle CAD = \angle CBD$
(Angles in the same segment)
Hence Proved.
Question 12. Prove that a cyclic parallelogram is a rectangle.
Answer:
Given:
ABCD is a parallelogram inscribed in a circle, i.e., it is a cyclic parallelogram.
To Prove:
ABCD is a rectangle.
Proof:
To prove that a parallelogram is a rectangle, we need to show that at least one of its interior angles is $90^\circ$.
Since ABCD is a parallelogram, we know that its opposite angles are equal.
$\angle A = \angle C$
... (i)
$\angle B = \angle D$
Since ABCD is a cyclic quadrilateral, we know that the sum of its opposite angles is $180^\circ$.
$\angle A + \angle C = 180^\circ$
... (ii)
Now, substitute the value of $\angle C$ from equation (i) into equation (ii):
$\angle A + \angle A = 180^\circ$
$2\angle A = 180^\circ$
$\angle A = \frac{180^\circ}{2} = 90^\circ$
Since one of the angles of the parallelogram ABCD is $90^\circ$, it must be a rectangle.
(We can also find the other angles: $\angle C = \angle A = 90^\circ$. Also, since consecutive angles in a parallelogram are supplementary, $\angle B = 180^\circ - \angle A = 180^\circ - 90^\circ = 90^\circ$, and $\angle D = \angle B = 90^\circ$.)
Therefore, a cyclic parallelogram is a rectangle.
Hence Proved.
Exercise 10.6 (Optional)
Question 1. Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Answer:
Given:
Two circles with centres O and O' intersect at two points B and C.
To Prove:
The line of centres OO' subtends equal angles at the two points of intersection B and C.
That is, $\angle OBO' = \angle OCO'$.
Proof:
Consider the triangles $\triangle OBO'$ and $\triangle OCO'$.
In the circle with centre O, OB and OC are radii.
OB = OC
(Radii of the same circle)
In the circle with centre O', O'B and O'C are radii.
O'B = O'C
(Radii of the same circle)
The line segment OO' is common to both triangles.
OO' = OO'
(Common side)
Therefore, by the Side-Side-Side (SSS) congruence rule, we have:
$\triangle OBO' \cong \triangle OCO'$
By CPCTC (Corresponding Parts of Congruent Triangles are Congruent), the corresponding angles are equal.
$\angle OBO' = \angle OCO'$
Hence, the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Hence Proved.
Question 2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Answer:
Given:
A circle with centre O.
Two parallel chords AB and CD, on opposite sides of the centre.
Length of chord AB = 5 cm.
Length of chord CD = 11 cm.
Distance between chords AB and CD = 6 cm.
To Find:
The radius of the circle.
Solution:
Let the radius of the circle be $r$.
Draw a perpendicular from the centre O to the chords. Since AB $\parallel$ CD, this perpendicular will pass through both chords, meeting AB at M and CD at N.
The perpendicular from the centre to a chord bisects the chord.
AM = MB = $\frac{AB}{2} = \frac{5}{2} = 2.5$ cm
CN = ND = $\frac{CD}{2} = \frac{11}{2} = 5.5$ cm
Let the distance OM be $x$. The distance between the chords is MN = 6 cm. Since they are on opposite sides, $MN = OM + ON$.
So, $ON = 6 - x$.
Now, consider the right-angled triangle $\triangle OMA$. By the Pythagorean theorem:
$OA^2 = OM^2 + AM^2$
$r^2 = x^2 + (2.5)^2$
$r^2 = x^2 + 6.25$
... (i)
Consider the right-angled triangle $\triangle ONC$. By the Pythagorean theorem:
$OC^2 = ON^2 + CN^2$
$r^2 = (6 - x)^2 + (5.5)^2$
$r^2 = 36 - 12x + x^2 + 30.25$
$r^2 = x^2 - 12x + 66.25$
... (ii)
From equations (i) and (ii), we can equate the expressions for $r^2$:
$x^2 + 6.25 = x^2 - 12x + 66.25$
$6.25 = -12x + 66.25$
$12x = 66.25 - 6.25$
$12x = 60$
$x = \frac{60}{12} = 5$ cm.
Now substitute the value of $x=5$ back into equation (i) to find the radius $r$:
$r^2 = (5)^2 + 6.25$
$r^2 = 25 + 6.25 = 31.25$
$r = \sqrt{31.25} = \sqrt{\frac{3125}{100}} = \sqrt{\frac{125}{4}} = \frac{\sqrt{25 \times 5}}{2} = \frac{5\sqrt{5}}{2}$ cm.
The radius of the circle is $\frac{5\sqrt{5}}{2}$ cm.
Question 3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
Answer:
Given:
A circle with centre O.
Two parallel chords with lengths 6 cm and 8 cm.
The smaller chord (6 cm) is at a distance of 4 cm from the centre.
To Find:
The distance of the other chord (8 cm) from the centre.
Solution:
Let the smaller chord be AB = 6 cm, and the larger chord be CD = 8 cm.
Let the radius of the circle be $r$.
First, we find the radius of the circle using the information about the smaller chord AB.
Draw a perpendicular from the centre O to chord AB, meeting it at M. This perpendicular bisects the chord.
$AM = \frac{AB}{2} = \frac{6}{2} = 3$ cm.
The distance of this chord from the centre is given as OM = 4 cm.
In the right-angled triangle $\triangle OMA$, by the Pythagorean theorem:
$OA^2 = OM^2 + AM^2$
$r^2 = 4^2 + 3^2$
$r^2 = 16 + 9 = 25$
$r = \sqrt{25} = 5$ cm.
So, the radius of the circle is 5 cm.
Now, we find the distance of the larger chord CD = 8 cm from the centre.
Draw a perpendicular from the centre O to chord CD, meeting it at N. This perpendicular bisects the chord.
$CN = \frac{CD}{2} = \frac{8}{2} = 4$ cm.
Let the distance ON be $d$.
In the right-angled triangle $\triangle ONC$, OC is the radius, so OC = 5 cm.
By the Pythagorean theorem:
$OC^2 = ON^2 + CN^2$
$5^2 = d^2 + 4^2$
$25 = d^2 + 16$
$d^2 = 25 - 16 = 9$
$d = \sqrt{9} = 3$ cm.
The distance of the other chord from the centre is 3 cm.
(Note: The problem does not specify if the chords are on the same or opposite sides of the centre. However, the calculation for the distance of the 8 cm chord from the centre is independent of this fact and will be 3 cm in either case.)
Question 4. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Answer:
Given:
A circle with center O.
An angle $\angle ABC$ with its vertex B located outside the circle.
The sides of the angle are two secants intersecting the circle at A, D and C, E respectively.
It is given that chord AD = chord CE.
To Prove:
$\angle ABC = \frac{1}{2} (\angle AOC - \angle DOE)$
Construction:
Join the points A and E to form the chord AE.
Proof:
Consider the triangle $\triangle ABE$.
The angle $\angle AEC$ is an exterior angle to $\triangle ABE$.
By the exterior angle theorem, the measure of an exterior angle is equal to the sum of the measures of the two opposite interior angles.
Therefore, $\angle AEC = \angle EAB + \angle ABE$.
We know that $\angle ABE$ is the same as $\angle ABC$.
So, $\angle AEC = \angle EAD + \angle ABC$. (Since $\angle EAB$ is the same angle as $\angle EAD$).
Rearranging this equation to find $\angle ABC$:
$\angle ABC = \angle AEC - \angle EAD$
... (i)
The angles $\angle AEC$ and $\angle EAD$ are inscribed angles.
The inscribed angle theorem states that the measure of an inscribed angle is half the measure of its intercepted arc.
$\angle AEC$ is the inscribed angle that intercepts arc AC. So, $\angle AEC = \frac{1}{2} (\text{measure of arc } AC)$.
$\angle EAD$ is the inscribed angle that intercepts arc DE. So, $\angle EAD = \frac{1}{2} (\text{measure of arc } DE)$.
Substitute these into equation (i):
$\angle ABC = \frac{1}{2} (\text{measure of arc } AC) - \frac{1}{2} (\text{measure of arc } DE)$
$\angle ABC = \frac{1}{2} [(\text{measure of arc } AC) - (\text{measure of arc } DE)]$
The measure of a central angle is equal to the measure of its intercepted arc.
So, measure of arc AC = $\angle AOC$, and measure of arc DE = $\angle DOE$.
Substituting these into the expression for $\angle ABC$:
$\angle ABC = \frac{1}{2} (\angle AOC - \angle DOE)$
The given condition that chord AD = chord CE implies arc AD = arc CE. This information is not needed for this proof but would be useful if we were asked to prove something else, for example, that $\triangle ABC$ is isosceles.
Hence Proved.
Question 5. Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Answer:
Given:
A rhombus ABCD, with diagonals AC and BD intersecting at point O.
To Prove:
The circle drawn with any side of the rhombus as diameter passes through the point of intersection O.
Proof:
Let's consider the side AB of the rhombus and the circle drawn with AB as its diameter.
A fundamental property of a rhombus is that its diagonals bisect each other at right angles ($90^\circ$).
Therefore, the angle at the intersection point O is a right angle.
$\angle AOB = 90^\circ$
Now, consider the geometric theorem for circles which states that the angle in a semicircle is a right angle. This means any angle subtended by a diameter at any point on the circumference is $90^\circ$.
Conversely, if a line segment (like AB) subtends a right angle at a point (like O), then that point O must lie on the circle with the line segment AB as its diameter.
Since $\angle AOB = 90^\circ$, the point O must lie on the circle drawn with AB as the diameter.
This reasoning applies to any side of the rhombus. For instance, for side BC, $\angle BOC = 90^\circ$, so O lies on the circle with diameter BC, and so on for all four sides.
Thus, the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Hence Proved.
Question 6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Answer:
Given:
ABCD is a parallelogram.
A circle passes through the vertices A, B, and C.
This circle intersects the line containing the side CD at a point E.
To Prove:
$AE = AD$.
Proof:
Since ABCD is a parallelogram, its opposite sides are parallel.
AB $\parallel$ DC
Since the point E lies on the line containing the segment DC, the line segment EC is parallel to AB.
AB $\parallel$ EC
We are given that A, B, C, and E are points on the circle. Thus, ABCE is a cyclic quadrilateral with one pair of opposite sides parallel (AB $\parallel$ EC).
A cyclic quadrilateral with a pair of parallel opposite sides is an isosceles trapezium.
In an isosceles trapezium, the non-parallel sides are equal in length. Here, the non-parallel sides are AE and BC.
AE = BC
... (i)
Now, since ABCD is a parallelogram, its opposite sides are equal.
AD = BC
... (ii)
From equations (i) and (ii), we can equate the values:
AE = AD
Hence Proved.
Question 7. AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
Answer:
Given:
A circle with chords AC and BD that bisect each other. Let their intersection point be O.
This means $OA = OC$ and $OB = OD$.
To Prove:
(i) AC and BD are diameters.
(ii) ABCD is a rectangle.
Proof:
Consider the quadrilateral ABCD formed by joining the endpoints of the chords.
Since the diagonals AC and BD bisect each other at O, the quadrilateral ABCD is a parallelogram. (A quadrilateral is a parallelogram if its diagonals bisect each other).
The vertices A, B, C, and D lie on the circle, which means that the parallelogram ABCD is a cyclic parallelogram.
We know that in a cyclic quadrilateral, the sum of opposite angles is $180^\circ$.
$\angle A + \angle C = 180^\circ$
Also, in a parallelogram, opposite angles are equal.
$\angle A = \angle C$
Substituting $\angle A$ for $\angle C$ in the cyclic property:
$\angle A + \angle A = 180^\circ$
$2 \angle A = 180^\circ$
$\angle A = 90^\circ$
Since one angle of the parallelogram is $90^\circ$, all its angles must be $90^\circ$. Therefore, ABCD is a rectangle.
(i) Proof that AC and BD are diameters
The angle subtended by a chord at the circumference is $90^\circ$ only if the chord is a diameter (Angle in a semicircle).
Since $\angle B = 90^\circ$, the angle subtended by chord AC at point B is $90^\circ$. Thus, AC is a diameter.
Since $\angle A = 90^\circ$, the angle subtended by chord BD at point A is $90^\circ$. Thus, BD is a diameter.
Hence, part (i) is proved.
(ii) Proof that ABCD is a rectangle
We have already proved that ABCD is a parallelogram and that one of its angles ($\angle A$) is $90^\circ$.
A parallelogram with one right angle is a rectangle.
Therefore, ABCD is a rectangle.
Hence, part (ii) is proved.
Question 8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90° – $\frac{1}{2}$ A, 90° – $\frac{1}{2}$ B and 90° – $\frac{1}{2}$ C.
Answer:
Given:
A triangle ABC is inscribed in a circumcircle.
AD, BE, and CF are the bisectors of $\angle A$, $\angle B$, and $\angle C$ respectively, intersecting the circumcircle at points D, E, and F.
To Prove:
The angles of triangle DEF are:
$\angle FDE = 90^\circ - \frac{A}{2}$
$\angle DEF = 90^\circ - \frac{B}{2}$
$\angle EFD = 90^\circ - \frac{C}{2}$
Proof:
We know that an inscribed angle is half the measure of its intercepted arc. Conversely, the measure of an arc is twice the inscribed angle that subtends it.
Since AD is the angle bisector of $\angle A$, we have $\angle BAD = \angle CAD = \frac{A}{2}$.
The arc BD is subtended by $\angle BAD$, so measure of arc BD = $2 \times \angle BAD = 2 \times \frac{A}{2} = A$.
The arc CD is subtended by $\angle CAD$, so measure of arc CD = $2 \times \angle CAD = 2 \times \frac{A}{2} = A$.
Similarly, since BE is the angle bisector of $\angle B$, measure of arc AE = measure of arc CE = $B$.
And since CF is the angle bisector of $\angle C$, measure of arc AF = measure of arc BF = $C$.
Now, let's find the angles of $\triangle DEF$.
1. Angle $\angle FDE$ (angle at vertex D):
The angle $\angle FDE$ subtends the arc FAE.
Measure of arc FAE = Measure of arc FA + Measure of arc AE = $C + B$.
$\angle FDE = \frac{1}{2} (\text{Measure of arc FAE}) = \frac{1}{2} (B+C)$.
In $\triangle ABC$, $A+B+C = 180^\circ$, so $B+C = 180^\circ - A$.
$\angle FDE = \frac{1}{2}(180^\circ - A) = 90^\circ - \frac{A}{2}$.
2. Angle $\angle DEF$ (angle at vertex E):
The angle $\angle DEF$ subtends the arc DAF.
Measure of arc DAF = Measure of arc DC + Measure of arc CF + Measure of arc FA? No, DAF = arc DA + arc AF. Let's use the other side. Angle $\angle DEF$ subtends arc FBD.
Measure of arc FBD = Measure of arc FB + Measure of arc BD = $C + A$.
$\angle DEF = \frac{1}{2} (\text{Measure of arc FBD}) = \frac{1}{2} (C+A)$.
Since $A+C = 180^\circ - B$, we have:
$\angle DEF = \frac{1}{2}(180^\circ - B) = 90^\circ - \frac{B}{2}$.
3. Angle $\angle EFD$ (angle at vertex F):
The arc subtended by $\angle EFD$ is arc ECD.
So, Measure of arc ECD = $A + B$.
$\angle EFD = \frac{1}{2} (\text{Measure of arc ECD}) = \frac{1}{2} (A+B)$.
Since $A+B = 180^\circ - C$, we have:
$\angle EFD = \frac{1}{2}(180^\circ - C) = 90^\circ - \frac{C}{2}$.
Thus, the angles of $\triangle DEF$ are $90^\circ - \frac{A}{2}$, $90^\circ - \frac{B}{2}$, and $90^\circ - \frac{C}{2}$.
Hence Proved.
Question 9. Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Answer:
Given:
Two congruent circles intersect each other at points A and B.
A line segment PAQ is drawn through A such that P lies on the first circle and Q lies on the second circle.
To Prove:
BP = BQ
Proof:
Consider the common chord AB for both circles.
Since the two circles are congruent, equal chords subtend equal angles at any point on the corresponding arcs of the circumference.
In the first circle, the chord AB subtends the angle $\angle APB$ at point P.
In the second circle, the same chord AB subtends the angle $\angle AQB$ at point Q.
Because the circles are congruent and the chord AB is common, the angles subtended by this chord at the circumference must be equal.
$\angle APB = \angle AQB$
Now, consider the triangle $\triangle BPQ$.
The angles $\angle BPQ$ and $\angle BQP$ are the same as $\angle APB$ and $\angle AQB$ respectively.
So, in $\triangle BPQ$, we have $\angle BPQ = \angle BQP$.
In a triangle, sides opposite to equal angles are equal in length.
The side opposite to $\angle BQP$ is BP.
The side opposite to $\angle BPQ$ is BQ.
Therefore, BP = BQ.
Hence Proved.
Question 10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Answer:
Given:
A triangle ABC.
The angle bisector of $\angle A$.
The perpendicular bisector of side BC.
To Prove:
The intersection point of the angle bisector of $\angle A$ and the perpendicular bisector of BC lies on the circumcircle of $\triangle ABC$.
Proof:
Let the angle bisector of $\angle A$ intersect the circumcircle of $\triangle ABC$ at a point D.
Since AD is the angle bisector of $\angle A$, we have:
$\angle BAD = \angle CAD$
We know that equal angles subtended at the circumference correspond to equal arcs. The angle $\angle BAD$ subtends arc BD, and the angle $\angle CAD$ subtends arc CD.
Therefore, arc BD = arc CD.
In a circle, chords corresponding to equal arcs are equal in length.
So, chord BD = chord CD.
Now, consider the triangle $\triangle BDC$. Since two of its sides are equal (BD = CD), it is an isosceles triangle.
The point D is equidistant from the points B and C.
The locus of all points that are equidistant from two given points (B and C) is the perpendicular bisector of the line segment joining them (BC).
Therefore, the point D must lie on the perpendicular bisector of BC.
From our initial assumption, D also lies on the angle bisector of $\angle A$ and on the circumcircle.
Thus, the intersection point of the angle bisector of $\angle A$ and the perpendicular bisector of BC is the point D, which lies on the circumcircle of $\triangle ABC$.
Hence Proved.

